 En anteriores capítulos de las aventuras de los Pitagóricos , que podéis ver aquí y aquí, nos acercamos al mundo geométrico de los matemáticos de la antigua Grecia y vimos cómo los números naturales, los de contar de toda la vida, eran representados con figuras geométricas formadas por piedrecitas o baldosas.
En anteriores capítulos de las aventuras de los Pitagóricos , que podéis ver aquí y aquí, nos acercamos al mundo geométrico de los matemáticos de la antigua Grecia y vimos cómo los números naturales, los de contar de toda la vida, eran representados con figuras geométricas formadas por piedrecitas o baldosas.
Esto está muy bien, sí, pero, ¿qué pasa con las cantidades no enteras? ¿Cómo se las arreglaban para representarlas?
Los pitagóricos conocían los números fraccionarios, de hecho, consideraban que el Universo entero podía describirse en términos de los números naturales y las fracciones entre ellos, aunque su forma de entender estas fracciones era un poco diferente a la que tenemos hoy en día.
Las magnitudes conmensurables
Ellos hablaban de magnitudes CONMENSURABLES y de razones entre ellas. Pero, ¿qué es esto de la conmensurabilidad? Se dice que dos segmentos AB y CD son conmensurables si existe un tercer segmento, que denotaremos por U (de unidad) que permite medir ambos segmentos de forma exacta. En el diagrama vemos que el pequeño segmento U cabe 5 veces exactas en AB y 3 veces exactas en el segmento CD. Decimos que la razón entre ambos segmentos es por tanto 3:5.
¿Cómo nos las apañamos para encontrar el segmento U que mida de forma exacta a dos segmentos cualesquiera AB y CD?
Los griegos disponían, cómo no, de un método para ello: EL ALGORITMO DE EUCLIDES. ¡Vamos a ver en que consiste!
En primer lugar, intentamos ver si el segmento más pequeño de los dos, en este caso CD, cabe un número de veces exacto en AB. Si esto fuera así tomaríamos U=CD que mediría tanto a AB como a CD.
Pero supongamos que CD cabe una cantidad de veces en AB, digamos 3, y sobra un trocito, un pequeño segmento al que denotaremos por EB. Es decir, AB = 3 × CD + EB.
Entonces necesitamos otro candidato para el segmento U. Tomamos para ello U=EB.
Si EB cabe un número exacto de veces en CD, entonces también cabe en AB, pues teníamos que AB estaba formado por 3 veces CD y una vez EB.
¿Qué ocurre si EB no cabe una cantidad exacta de veces en CD?
Supongamos que cabe 4 veces, pero sobra un trocito al que denotamos FD. Entonces podríamos repetir el proceso y ver si haciendo U=FD este cabe un número exacto de veces en EB. Si esto es así y cabe, digamos, 2 veces en EB, entonces como CD estaba formado por 4 veces EB y el trocito FD tendríamos que cabe 4 × 2 +1 = 9 veces en CD. Y como CD cabía en AB 3 veces y sobraba el trocito EB, tenemos que FD cabe 3 × 9 + 2 × 1 = 29 veces en AB. ¡Ya hemos encontrado el segmento U!
Esto que hemos realizado visualmente con segmentos también podemos hacerlo numéricamente cambiando estos segmentos por un valor, digamos AB=87 y CD=27.
Los pasos dados anteriormente serían dividir 87 entre 27, nos da cociente 3 (las tres veces que cabía CD en AB) y resto 6 (el segmento EB). Dividimos ahora 27 entre 6 (esto es para ver cuántas veces cabe el pequeño segmento EB en CD) lo que da cociente 4 y resto 3 (el segmento FD) y finalmente dividimos 6 entre 3 (esto es para ver cuántas veces cabe FD en EB) y obtenemos una división exacta. Así que el divisor para el que la división fue exacta es nuestro segmento U=3.
Pero si nos damos cuenta lo que hemos hecho es buscar el número más grande que divide de forma exacta a AB=87 y CD=27 ¡Efectivamente, el Máximo Común Divisor de 87 Y 27!
Sin embargo, en la escuela todos aprendimos una regla diferente para calcular el Máximo Común Divisor. Haciendo memoria recordamos que descomponíamos los números en factores primos (números que solo se pueden dividir de forma exacta entre 1 y ellos mismos), obteniendo 87= 3 × 29 y 27 = 33, y decíamos aquello de “factores comunes al menor exponente” que en este caso es 3, esto es, MCD (87, 27) = 3.
Hemos calculado el Máximo Común Divisor de dos formas distintas: utilizando el algoritmo de Euclides que es esencialmente geométrico, y utilizando la descomposición de un número en factores primos, es decir, de forma puramente ARITMÉTICA.
Los pitagóricos creían que, dadas dos magnitudes cualesquiera, estas siempre eran CONMENSURABLES, ya que si dos magnitudes admiten una tercera que las mide de forma exacta, digamos m y n veces respectivamente, la razón entre estas magnitudes es la fracción m / n. Los pitagóricos creían que cualquier magnitud se podía expresar utilizando los números naturales y las fracciones. ¿Es esto así?
Pitágoras no quería ni oír hablar de la posible existencia de magnitudes inconmensurables, perdía la paciencia y los papeles cada vez que uno de sus discípulos insinuaba lo contrario.
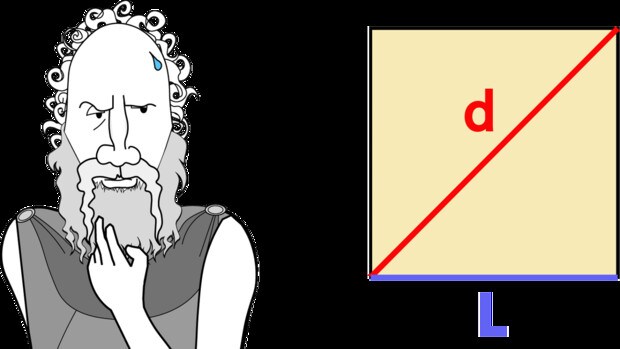
Hípaso de Metaponto, uno de estos discípulos, dedicó buena parte de su investigación a la búsqueda de la conmensurabilidad del lado y la diagonal del cuadrado, pero cuanto más tiempo dedicaba a este problema, más convencido estaba de que era imposible resolverlo. Finalmente demostró que el lado y la diagonal son INCONMENSURABLES.
Las consecuencias que tuvo este descubrimiento para su autor fueron nefastas. Su hallazgo ponía en riesgo los pilares de la escuela pitagórica. Para protegerlos, se decretó el más estricto de los silencios. Pero Hípaso no pudo esconder mucho tiempo una verdad de tal envergadura, no fue capaz de ocultar el descubrimiento de su vida y acabó gritando sus resultados a quien quisiera escucharlos. Cuenta la leyenda que el propio Pitágoras arrojó por la borda de un barco al pobre deslenguado, aunque otras fuentes más benévolas dicen que solo fue desterrado de la escuela.
Pero no nos despistemos de las matemáticas. ¿Cómo se sabe que el lado y la diagonal de un cuadrado son inconmensurables?
Desde la perspectiva actual, si el lado del cuadrado mide 1 unidad, podemos aplicar el teorema de Pitágoras para obtener que la diagonal mide raíz de 2 unidades:
De este modo la razón entre ambas magnitudes es:
Y hoy en día todos sabemos que
es un número irracional, esto es, que no se pude escribir como fracción. De hecho, la demostración que se da normalmente en los libros de texto sobre este hecho es por REDUCCIÓN AL ABSURDO: suponer lo contrario de lo que queremos probar y llegar a una contradicción, por lo que nuestro enunciado original habrá de ser cierto.
No nos podemos resistir a incluirla en estas líneas aún a riesgo de perder la atención del lector, pero avisamos con un pequeño spoiler que, si bien la demostración puede ser un poco técnica, acto seguido haremos una versión geométrica y visual del tipo ¡MIRA!
Para la primera demostración (que de hecho aparece en los famosos Elementos de Euclides del año 300 a. C. aproximadamente) utilizaremos de nuevo el Teorema de factorización única (también llamado Teorema Fundamental de la Aritmética) que dice todo número se descompone como producto de números primos de forma única.
Supongamos pues que raíz de dos es una fracción:
que supondremos irreducible, es decir, que no se puede simplificar. Si esto es así y descomponemos p y q en factores primos no pueden tener ninguno en común, pues si los tuviéramos podríamos simplificar la fracción tachando los factores comunes.
Pero ahora ocurre una cosa extraña, si p tiene ciertos factores primos, p^2 tendrá los mismos factores repetidos dos veces así que tendrá una cantidad par de factores primos, y lo mismo ocurre con q^2 que también tendrá una cantidad par de factores primos.
Pero en la ecuación
si elevamos ambos miembros al cuadrado obtenemos
que equivale 2q^2=p^2. Pero en la derecha tenemos un número con una cantidad par de factores primos y en la izquierda tenemos ¡una cantidad impar de factores primos! Los factores primos de q^2que eran una cantidad par y un 2. ¡CONTRADICCIÓN!
No sé si los lectores han seguido esta prueba, pero lo esencial es que es de carácter ARITMÉTICO al igual que el método de calcular el máximo común divisor que aprendimos en el colegio.
Pero los Pitagóricos eran esencialmente geómetras y al igual que el algoritmo de Euclides permite calcular el MCD de forma “geométrica” vamos a ver una demostración de la irracionalidad de
simplemente con la noción de conmensurabilidad, esto es, ¡PURAMENTE GEOMÉTRICA!
¡Vamos allá! La demostración también es por reducción al absurdo así que imaginemos que el lado y la diagonal del cuadrado son conmensurables, esto es, existe un segmento U que mide a ambos de forma exacta.
Podemos trazar una circunferencia con centro en la esquina inferior izquierda del cuadrado y radio el lado del cuadrado. Esta circunferencia corta en un punto a la diagonal dividiéndola en dos segmentos.
Estos dos segmentos también pueden medirse con el segmento U de forma exacta ya que uno de ellos es precisamente el lado del cuadrado en el que cabe una cantidad exacta de veces el segmento U.
Trazamos por este punto una perpendicular a la diagonal hasta cortar al lado vertical derecho del cuadrado. De este modo construimos un nuevo cuadrado cuyo lado es el segmento menor de la diagonal.
Trazamos un segmento con extremos la esquina del cuadrado pequeño y la esquina inferior izquierda. Obteniendo dos triángulos.
Afirmamos que estos dos triángulos son idénticos. En efecto, basta para ello ver que tienen dos lados y un ángulo iguales. Ambos triángulos tienen un lado en común y otro lado que coincide con el lado del cuadrado. Además, ambos tienen un ángulo recto.
Así que los otros dos lados de ambos triángulos también son iguales y además como uno de ellos es justamente el lado del cuadrado pequeño también es igual al trocito pequeño de la diagonal en el que cabía U de forma exacta.
Pero entonces, dado que el lado del cuadrado grande se mide de forma exacta con U y este trozo vertical también, el resto que coincide con la diagonal del cuadrado pequeño también admite al segmento U una cantidad exacta de veces.
¿Qué hemos conseguido? Partíamos de un cuadrado cuyo lado y diagonal se medían de forma exacta con U y hemos construido otro cuadrado más pequeño cuyos lados y diagonal también se miden de forma exacta con U. Pero ahora podemos repetir el argumento al cuadrado pequeño y encontrar otro cuadrado más pequeño para el que U también mide su lado y diagonal y otro más pequeño y otro…
Sin embargo, el segmento U ya se había fijado al principio, y los nuevos cuadrados son cada vez más pequeños hasta que sean incluso de lado menor que U. ¿Cómo vamos a medir el lado y la diagonal de un cuadrado con un segmento que es mayor que ellos?
La contradicción a la que hemos llegado parte de suponer que el lado y la diagonal del cuadrado original eran conmensurables así que esto es imposible.
¡PURA GEOMETRÍA!
Como despedida os dejamos unos enlaces en los que podéis consultar los elementos de este artículo en formato vídeo ¡Hasta luego!
MÁXIMO COMÚN DIVISOR
EL ALGORITMO DE EUCLIDES
RAÍZ DE DOS ES IRRACIONAL
Urtzi Buijs es Profesor Titular del área de Geometría y Topología en la Universidad de Málaga. Miriam González es Desarrolladora de Software en la Universidad de Málaga. Ambos son fundadores del canal de Youtube Archimedes Tube.
El ABCdario de las Matemáticas es una sección que surge de la colaboración con la Comisión de Divulgación de la Real Sociedad Matemática Española (RSME).
