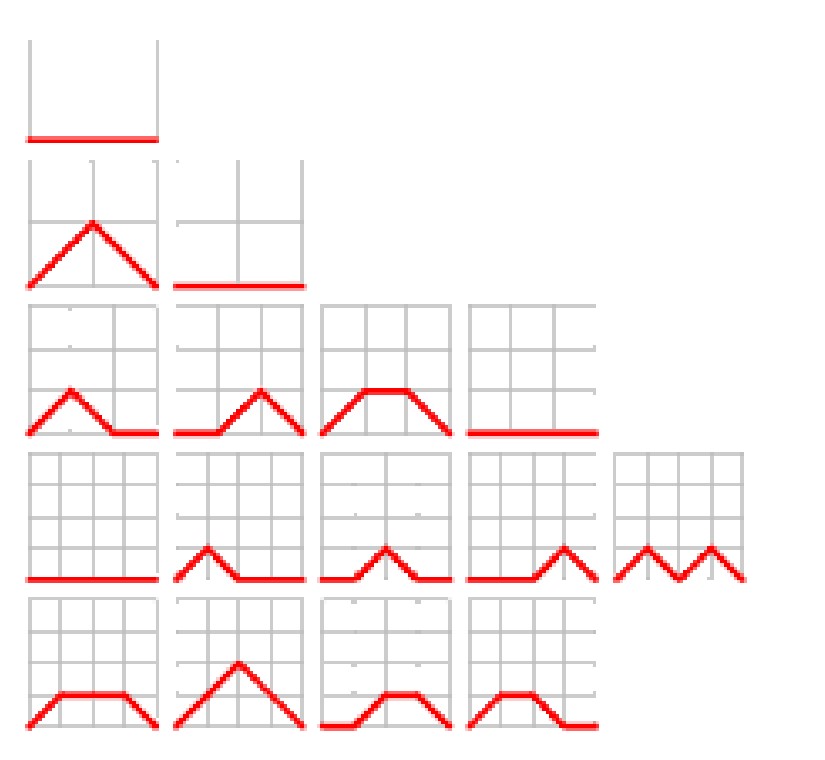
¿Cuál es el quinto número de Motzkin?, nos preguntábamos la semana pasada. He aquí la respuesta de Manuel Amorós: “Vamos a razonar para obtener de forma recursiva M(5), el número de Motzkin para 5 puntos. Consideremos un vértice determinado V. Pueden pasar dos cosas: desde ese vértice sale alguna cuerda o no sale ninguna. En el segundo caso dicho vértice no interviene en las formas de unir los cuatro puntos que quedan, y por tanto tenemos M(4) opciones. Si una cuerda sale de V dividirá el círculo en dos partes independientes, ya que no podemos atravesarla. Podemos combinar las posibilidades a ambos lados, que son a su vez números de Motzkin, donde se descuentan los dos vértices de la cuerda separatoria. Resumiendo: M(5) = M(4) + M(0)*M(3) + M(1)*M(2) + M(2)*M(1) + M(3)*M(0). Sustituyendo los valores conocidos M(0) = 1, M(1) = 1, M(2) = 2, M(3) = 4, M(4) = 9, obtenemos: M(5) = 9 + 4 +2 + 2 + 4 = 21″.